Description:

一个N×M的数表中第i行第j列上的数定义为

，

有多组询问，每次询问数表中不超过A的元素和。

Solution:

定义数表中第i行第j列的数是a[i][j]，很容易发现a[i][j] = a[d][d] (d = gcd(i, j))

那么我们要求的答案就是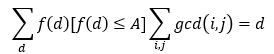f(d)表示的是d的约数和

变换一下得到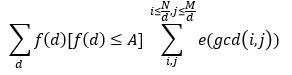

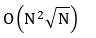卷积一下，到这里我们就得到了一个的算法

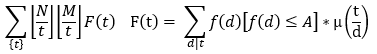
考虑离线做法

如果我们已知了F(t)的前缀和的话，显然可以每次根号N地求出答案

同时我们有f(d) <= A的限制。

离线按照A排序，用树状数组维护F(t)的前缀和。

从询问(N,M,A) -> 询问(N',M',A')时，我们需要把所有的值在(A,A']内的f(d)全部插入进去，

显然一个f(d)只会被插入一次，一个f(d)可以更新的F(t)是logN的。

这样我们就得到了一个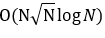的做法

#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
const int MAXN = 100010;
pair<int, int> f[MAXN];
int a[MAXN], Answer[MAXN];
int T, N, M, A; bool vis[MAXN];
int divisor[MAXN][200], cnt[MAXN];
int prime[MAXN], miu[MAXN], tot;
struct Tque
{
	int N, M, A, id;
	Tque() {}
	Tque(int _id, int _N, int _M, int _A)
	{ id = _id; N = _N; M = _M; A = _A; }	
} Que[MAXN];
bool cmpA(Tque a, Tque b) { return a.A < b.A; }
void Modify(int x, int y) { for(; x <= 100000; x += x & -x) a[x] += y; }
int Query(int x) { int ret = 0; for(; x; x -= x & -x) ret += a[x]; return ret; }
int main()
{
	freopen("table.in", "r", stdin);
	freopen("table.out", "w", stdout);

	for(int i = 1; i <= 100000; ++i)
		for(int j = 1; j <= 100000; ++j)
		{
			if((long long) i * j > 100000) break;
			divisor[i * j][cnt[i * j]++] = i;
		}
	for(int i = 1; i <= 100000; ++i)
		for(int j = 0; j < cnt[i]; ++j) f[i].first += divisor[i][j];
	for(int i = 2; i <= 100000; ++i)
	{
		f[i].second = i;
		if(!vis[i]) prime[tot++] = i, miu[i] = -1;
		for(int j = 0; j < tot; ++j)
		{
			if((long long) i * prime[j] > 100000) break;
			vis[i * prime[j]] = 1; miu[i * prime[j]] = -miu[i];
			if(i % prime[j] == 0) { miu[i * prime[j]] = 0; break; }
		}
	}
	scanf("%d", &T); miu[1] = f[1].second = 1; sort(f + 1, f + 100001); 
	for(int i = 1, x, y, z; i <= T; ++i)
		scanf("%d%d%d", &x, &y, &z), Que[i] = Tque(i, x, y, z);
	sort(Que + 1, Que + T + 1, cmpA);
	for(int i = 1, p = 1; i <= T; ++i)
	{
		int Lim = min(N = Que[i].N, M = Que[i].M), ans = 0; A = Que[i].A;
		for(int d = f[p].second; p <= 100000 && f[p].first <= A; d = f[++p].second)
			for(int k = 1; (long long) d * k <= 100000; ++k) Modify(d * k, miu[k] * f[p].first);
		for(int l = 1, r; l <= Lim; l = r + 1)
			Answer[Que[i].id] += (Query(r = min(N / (N / l), M / (M / l))) - Query(l - 1)) * (N / l) * (M / l);
	}
	for(int i = 1; i <= T; ++i) printf("%d\n", Answer[i] & 0x7fffffff);
	return 0;
}

Hint:

考场上只想出60分的暴力= =根本没想去离线。。真是太悲伤了。。

卧槽latex代码在这里竟然没用(?)一张一张写出来截图真是蛋疼= =