傻逼后缀数组|Manacher写不对

傻逼斜率优化调不出

傻逼费用流(也许是错的？)不停跪

历程结束，自挽

逢考必病。。这病还能不能治了。。。

一个公式

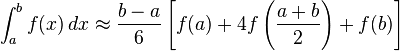
然后一个结论

如果利用Simpson公式计算的[a,b]的面积与[a,m]+[m,b]的面积相差无几，那么就可认为原图像的面积就是[a,b]的面积

因为我们是理论计算机xxxx。。所以二分地计算图形面积，直到满足上面那个结论或精度xxx的时候就停下来，

这样就完成了计算。。

Description

给一个序列(<=2*10^5)，求问最长的字典序最小的一个序列的子串，该子串满足如下性质：将该子串的所有元素取出组成与子串长度相等的新数列，在新数列中至多添加K个数字，使得数列为D等差数列，D等差数列即数列为等差数列且公差为D。

没参加比赛。。因为不是周末晚上家里没网。。。（很奇怪的性质对不对。。。

Description

要求一个数据结构，支持：

A：在容器末尾插入一个向量(x,y)

Q：询问容器(l,r)的区间里的所有向量，与向量(x,y)点积最大的是多少

操作数N在4*10^5范围内，保证答案在64位整数范围内，强制在线

A类数据：30分，N<=1000

B类数据：10分，插入向量横坐标单增且总是询问整个区间

C类数据：20分，插入向量坐标单增

D类数据：10分，总是询问整个区间

E类数据：20分，离线

F类数据：10分，无特殊条件

Description:

有10^5个点10^5个操作。

每个点有两个属性：权值和颜色(颜色值小于C)。

操作分为四种：1.CW修改一个点的权值。2.CC修改一个点的颜色。3.QS询问u->v路径上与u颜色相同的点的权值和。4.QM询问u->v路径上与u颜色相同的点的权值极值。保证u和v的颜色相同

数据范围：

Description

给定一个长度不超过1200的整数N，问从1~N的范围里有多少个整数的子串不包括S集合里的任何串。

|S|<=50,S集合中的所有串的长度和在1500范围内。样例：Input: 20 3 2 3 14 Output: 14 解释：1~20中不包含{2,3,14}的显然有{1,4,5,6,7,8,9,10,11,15,16,17,18,19}这么多

Description:

一个长度小于700的数列，每个数有三个都是正整数的属性：权值a，删除代价b，附加属性c。

我们要求一个最小代价的删除方案，使得附加属性的字典序最小，并且使新数列权值构成的最长上升序列至少比原数列权值构成的最长上升数列的答案少1

Description:

一个N×M的数表中第i行第j列上的数定义为

，

有多组询问，每次询问数表中不超过A的元素和。